Absolute Knowledge
It is sometimes obvious to us that something is evidently true. However, how do we know that something is true with absolute certainty. Let us consider some examples.
Example 1: 1 + 2 = 3
Here is the first one:
1 + 2 = 3
Question: How can we show that this proposition is actually true? Keep in mind, what we are asking here is not how we as human beings historically came to discover that one plus two equals three. Instead, the question is how do we know this proposition is true? How is it justified?
While it might be argued that it probably took centuries of human experience with the world before this proposition occurred to our ancestors, it could be argued that we do not need any experiments or observations to justify this proposition. Indeed, we do not need to conduct any experiments or observations in order to establish that one plus two actually equals three at all times. But if it is not based on experience, then what is it based on? The answer is: the truth of this proposition stems from the very meanings of the terms “two,” “three,” “plus,” and “equals.” What do we mean by “two”? Setting aside the question of a precise mathematical definition of the concept, we can say that “two” roughly means something like “one and another one.” The same goes for the concept of “three,” which is essentially short for “one, another one, and another one.” But if that is what we mean by “two” and “three,” then it follows that one plus two equals three.
This kind of reasoning is called deduction. In other words, this proposition holds true as long as “two,” “three,” and other terms are understood in the way that they are usually understood. Importantly, we do not need to conduct any experiments or observations to ascertain that one plus two equals three at all times and in all places, for the proposition is true by virtue of the definitions of its terms.

Example 2: All Swans Are White
Now, consider another example:
All swans are white.
How do we know this? Once again, the question is not when and under what circumstances humans first came to appreciate the truth of the statement. Rather, the question is how can this proposition be justified? What makes it true?
The intuitive answer is that this should have to do with experience; surely, one cannot know anything about the colour of swans unless one goes out and observes some actual swans! To establish that all swans are white, one should first observe the colours of individual swans and record the results of these observations. Now, suppose we go out and find a white swan. We formulate this in a singular proposition that describes our experience:
Swan a is white.
We then find two more swans, observe that they are also white, and record this in the following two propositions:
Swan b is white.
Swan c is white.
Based on the results of these observations, we generalize and conclude that all swans are white. This inference from individual instances to a general proposition is called induction.
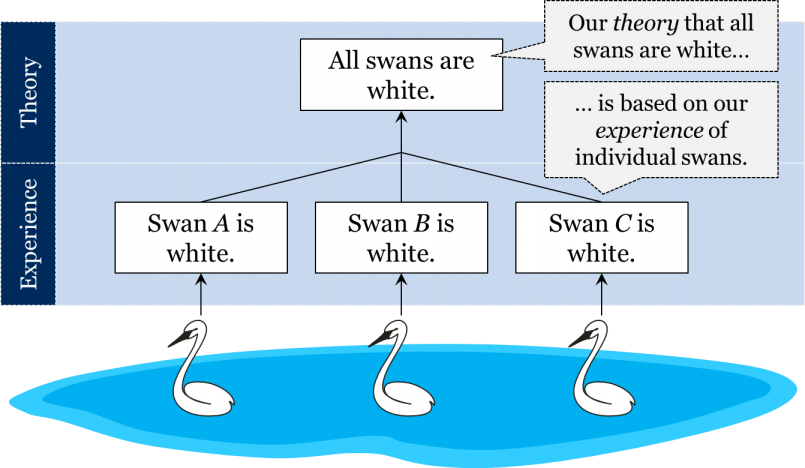
In short, we seem to agree that the proposition “all swans are white” is justified by experience: it is an inductive generalization of the results of our observations of individual swans.
Example 3: The Law of Universal Gravitation
Our third and final example is from physics—the law of universal gravitation:
[latex]\begin{gathered} F=G\frac{m_1m_2}{r^2} \end{gathered}[/latex]
Here, F stands for the force of attraction between two material objects, m1 and m2 are the respective masses of these two objects, r is the distance between them, and G is a constant that we can ignore here. The law says that there is a force of attraction between any two objects in the universe: the greater the masses of these objects, the greater the force of attraction between them; the greater the distance between them, the smaller the force. In other words, the attraction between two objects increases with mass and decreases with distance. The same idea can be expressed in more technical terms: the force of gravity is proportional to the product of the two masses and is inversely proportional to the square of the distance.
Now, how can we justify this proposition? How do we know it is true? More specifically, can the law of gravity be justified independently of experience, simply by virtue of the definitions of its terms, or does it take some experiments and observations to justify it? Is it more similar to “one plus two equals three” or “all swans are white”? In other words, is it possible to show that this proposition is true simply by analysing the definitions of “force,” “mass,” and “distance,” or should we actually go out there and see how objects in the world behave in order to justify the law?
If we pay attention to the concepts of “force,” “mass,” and “distance,” there is nothing there that suggests that all objects should attract each other with a force proportional to the product of the masses and inversely proportional to the square of the distance. In fact, we could conceive of an infinite number of different propositions which use the exact same concepts of “force,” “mass,” and “distance.” For instance, we could say that the force of gravity is proportional to the sum of the masses, or that it is inversely proportional to the cube of the distance, or that it increases with distance:
[latex]\begin{gathered} F=G\frac{m_1m_2}{r^2} \end{gathered}[/latex]
Thus, there is no way to deduce the law of gravity merely from the definitions of its concepts, for there is clearly more than one way in which these concepts could be put together. But then how do we know which one of these numerous possibilities is true? The intuitive answer is that we have to go out and observe: there is simply no other way to know which one of these is the case without conducting experiments and observations. How might we do it? Perhaps if we were to observe that it holds for the Earth and a falling apple and also to observe that it holds for the Earth and the Moon, the Sun and Jupiter, and any two planets, then we could generalize and conclude that it holds between any two objects in the universe.
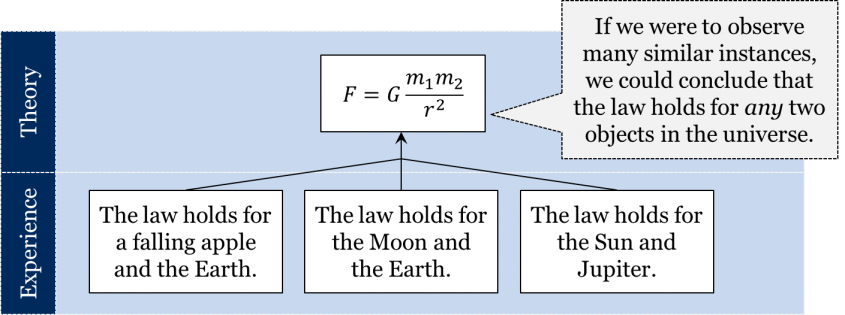
What Does All This Mean?
In brief, the mode of justification of the law of gravity appears to be intuitively similar to that of “all swans are white.” The fact that the law of gravity can be expressed as a mathematical equation should not confuse us here. It makes no difference how the proposition is expressed: the same proposition can be expressed mathematically or in a natural language, but that does not change the gist of the proposition. The same proposition can be expressed as “1 + 2 = 3” or as “one plus two equals three”—its truth follows from the definitions of its concepts regardless of how we express it. Similarly, we have seen how the law of gravity could be expressed both as a mathematical equation and as “the force of gravity is proportional to…”—it makes no difference. The important point here is that one needs to conduct experiments and observations to check if the law is true.
Media Attributions
Unless otherwise noted, all figures are from the chapter “Absolute Knowledge” in the book Introduction to History and Philosophy of Science by Barseghyan et al., via eCampusOntario and are used under a CC BY 4.0 license.

