15 Two Questions of Absolute Knowledge

Now that we understand the difference between analytic and synthetic propositions, we must specify the main question of this chapter for the two types of propositions:

• Can analytic propositions be absolutely certain?
• Can synthetic propositions be absolutely certain?

Let’s first consider the former. Is it possible to establish the truth of an analytic proposition beyond any doubt? For instance, can the propositions of math or logic be proven with absolute certainty? The short answer is “yes”, because analytic propositions are either definitions or follow from definitions and, thus, they unfold what is already in a sense implicit in the definitions. Insofar as we stick to a given set of definitions, any analytic proposition that follows from them will be absolutely true. For example, as long as “bachelor” is defined as “an unmarried man”, the proposition “all bachelors are unmarried” will remain absolutely certain. Similarly, as long as we stick to the definitions (including the postulates) of Euclid’s geometry, its propositions will always hold.

This is equally true for any analytic proposition and, consequently, any theory that consists of only analytic propositions. Therefore, the answer to our first question is “yes”: there can be absolutely certain analytic propositions. As a result, we can legitimately speak of mathematicians or logicians proving a certain theorem beyond any reasonable doubt.

Now, what about synthetic propositions: can they ever be absolutely certain? Can our hypotheses about the workings of the world ever be proven beyond any reasonable doubt? In other words, can we have absolutely certain theories in physics, chemistry, biology, psychology, sociology, economics, etc.? The short answer to this question is “no”. To appreciate this, we have to consider how synthetic propositions are justified and what problems their mode of justification faces.

As we have seen with the example of white swans and the law of gravity, synthetic propositions must somehow be based on experience. So intuitively, we are inclined to think that the justification of a synthetic proposition requires some experience – some experiments and/or observations. This goes for both singular synthetic propositions, such as “swan a is white”, and general synthetic propositions, such as “all swans are white”. Indeed, how else can we justify any of these synthetic propositions, unless we go out there and observe?

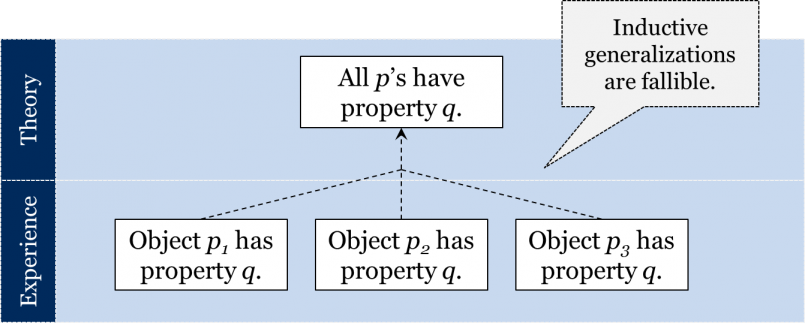
Intuitively, we are inclined to accept the following general template. In order to justify a synthetic proposition, we find an object, let’s call it p1, and observe that it has some property q. We then find a similar object p2 and observe that it has the same property q. We repeat this with more objects of the same class – more p’s – and conclude that all objects of type p have property q.

But precisely because all synthetic propositions must eventually be based on experience, they cannot be absolutely certain. There are three giant obstacles that prevent synthetic propositions from being established beyond any reasonable doubt: the problem of sensations, the problem of induction, and the problem of theory-ladenness.

Problem 1: Sensations

First, let us distinguish between the human mind and the world outside of the human mind. Our feelings, emotions, sensations, theories, thoughts, beliefs, ideas, etc. are all in the mind. However, plants, animals, other people, and the Earth itself, as they exist in reality and independently of the human mind, are in the external world. So, our sensations of swans will always be in our minds. Swans as they exist “out there”, objectively, should not be confused with my sensations of swans, which exist in my mind. In other words, things as they exist in reality should not be confused with things as we perceive them:

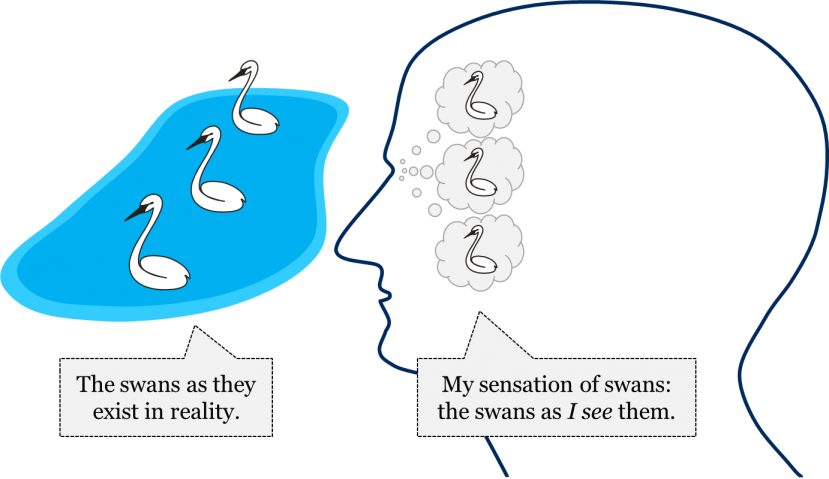
In order to claim that the proposition “all swans are white” is absolutely certain, we have to first establish that our sensations of swans are absolutely trustworthy: we have to make sure that swans as we see them are exactly the same as swans as they exist independently of the human mind. But how can we make sure that swans as we see them are exactly as they are in reality? How can we ever ascertain that our sensations convey the exact image of things as they really are?

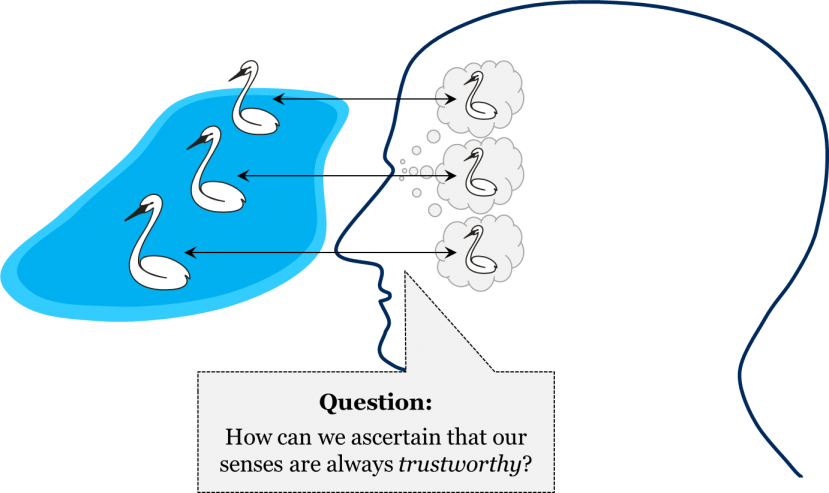
There are reasons to suspect that our senses are not always trustworthy; surely, we don’t normally trust everything we perceive when we are not sober! So, the question of the trustworthiness of our senses is far from idle; if we are going to claim that any of our hypotheses about the external world are absolutely certain, we have to prove that our sensations convey to our minds exact images of the things as they really are.

Suppose I see a cup of coffee in front of me. This is my visual sensation of a cup of coffee. How can I possibly make sure that there is really a cup of coffee in front of me? I could approach the cup and pick it up, smell it, and taste it. In other words, I could try to confirm my visual sensations with my sensations of touch, smell, and taste. Now, suppose that my sensations of touch, smell, and taste also suggest that there is a cup of coffee in front of me. Will this guarantee that there is really a cup of coffee in front of me? Of course, not! All it would demonstrate is that my visual, tactile, olfactory, and gustatory sensations cohere with one another. That’s all! But the question was not whether my sensations are in agreement with one another. The question was whether my sensations are absolutely trustworthy.

In order to be absolutely sure that the cup of coffee is real, I would somehow have to grasp what the cup is like using a means that bypassed my senses. But that is impossible! We don’t have a way of getting in touch with the world without using our senses. So even when all my senses seem to suggest that there is a cup of coffee in front me, all it really tells me is that I sense that there is a cup of coffee in front of me.

What if we asked other people to confirm the presence of the cup? Would that solve the problem? No, it would not. After they observed the cup, they would have to somehow convey the results of their observations to me. There is no way for me to receive their message that does not somehow involve my senses. On top of the fact that other people are relying on their senses, I have to rely on my senses to communicate with them about the information they gathered through their senses. So, all this would tell me is that I have an additional sensation that agrees with my other sensations.

The same goes for any tools we might want to use to confirm our sensations. Suppose I was to use some kind of a coffee detector to ascertain that there is a cup of coffee in front of me. Say, the coffee detector had a screen that would display the message “this is coffee”. Would that solve the problem? No, since I would have to read the screen or otherwise interact with the detector and the only way I can do that is though my senses – visual, auditory, etc. Therefore, I would only have one more sensation that is coherent with my other sensations.

In short, in order to be in a position to say that there is a cup of coffee in front of me, I have to be absolutely sure that my senses conveyed the exact picture of the cup as it really is. Yet, this cannot be guaranteed. All I can check is that my sensations are in agreement with one another, but that doesn’t necessarily guarantee that the world out there is exactly as my sensations suggest. This is known as the problem of sensations: there is no guarantee that senses convey the exact picture of things as they really are.

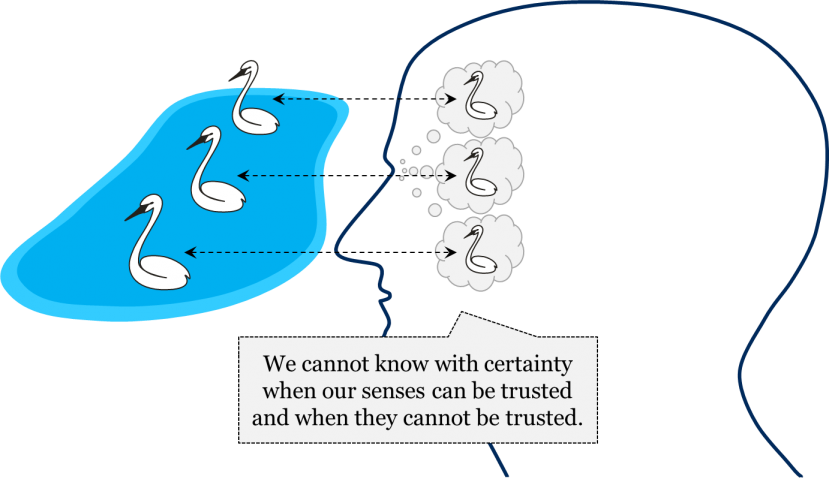
It is even possible that we might be living in a computer simulation; we just don’t have an absolutely certain way of knowing that we aren’t! While there have been many attempts to solve the problem of sensations, it is accepted nowadays that strictly speaking it cannot have a solution.

One suggested solution was to argue that because our senses are a product of evolutionary processes, they have adapted to perceive the world correctly, for otherwise humans wouldn’t survive. Is this a good solution? No, it’s not, because it is based on the theory of natural selection, which is itself an empirical theory; the proposition “our senses adapt to their environment” is a synthetic proposition which can only be justified by invoking knowledge obtained with the use of our senses. Thus, the solution is itself circular: in order to show that our senses are trustworthy it invokes the theory of natural selection, but in order to justify the theory of natural selection we need to rely on evidence obtained with our senses.

Importantly, the problem of sensations in general doesn’t mean that we cannot trust our senses; not trusting our senses wouldn’t be particularly conducive to our survival. The point here is not that our senses are deceiving us – no! The point is that we just cannot be absolutely sure that they are not deceiving us. There is a very important difference here: it’s one thing to claim that senses are not trustworthy, it’s another thing to claim that we cannot know whether they are trustworthy or not. The problem of sensations is all about the latter: it tells us that we simply cannot be absolutely sure that our senses are not deceiving us.

Problem 2: Induction

Suppose for the sake of argument that there is no problem of sensations; suppose that our senses are absolutely trustworthy and convey the picture of the world as it really is. Even if we were to make this assumption, we would still be facing a serious problem. Anytime we observe something, the outcome is a singular synthetic proposition, such as “swan a is white” or “swan b is white”. Question: how can we ever prove any of our general synthetic propositions if the outcomes of our observations are always singular propositions? In other words, how is it possible to claim that all swans are white if our observations only tell us that individual swans we have observed so far are white? Is there any guarantee that there won’t be any non-white swans out there (as black swans do exist in nature)? Similarly, how can we ever be sure that the law of gravity has been proven beyond any doubt? As a general synthetic proposition, it must be based on observations, but all our observations concern individual cases. We can observe that the law holds between the Earth and the Sun, or the Sun and Jupiter, and so on, but does this prove that the law holds for any two objects in the universe? In other words, how can we be sure that our inductive generalizations hold water?

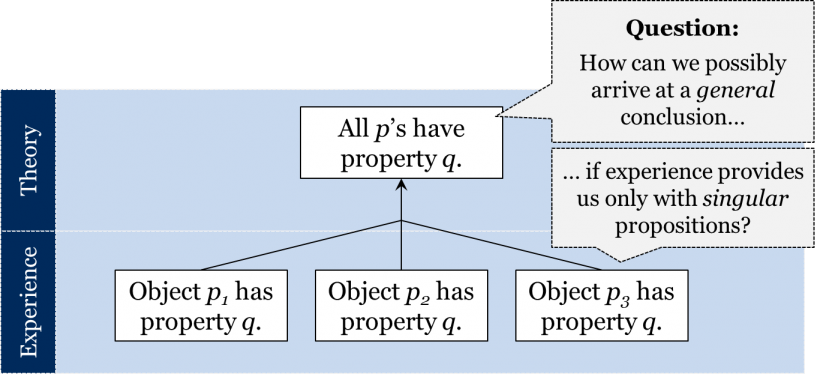
Because general propositions refer to all objects within a given class, they attempt to say something not only about those objects that we have already observed, but any object of that type. To establish “all swans are white” beyond any reasonable doubt we should make sure we have observed each and every swan out there, including all swans that have ever lived and all swans that will be born in the future. Surely, this is impossible! But if we are never in a position to observe all swans, how can we be absolutely sure that all swans are white? It would suffice to observe one counterexample – one non-white swan – and the whole generalization would fall apart. Thus, no matter how many millions of white swans we have managed to observe, there is no logical proof that the swans we will observe in the future will also be white. Similarly, we can observe millions of instances of objects acting in accord with the law of gravity, but this doesn’t prove that all objects in the universe obey this law. Even if all the physicists in the world were to collect their observational results in a huge database, the outcome would still be limited; it would never cover all objects in the universe.

This is the gist of the problem of induction: because our experience is always limited, our inductive generalizations are inevitably fallible.

The only exceptions here are those rare cases, where the number of objects within a class is finite and we have managed to observe each and every one of them. For example, the proposition “all capitals of Rus’ (a kingdom in medieval Europe) were located between 45° and 60° northern latitude” doesn’t face the problem of induction, since Rus’ had a finite number of capitals and all of their locations are known. However, in most cases, there are so many objects within a class that we simply cannot observe all of them. In those numerous cases, our generalizations remain fallible because of the problem of induction.

Now, is there a way to solve the problem of induction? One classic attempt to solve the problem was to invoke the so-called principle of the uniformity of nature – the idea that in similar circumstances objects of the same class behave similarly. According to this principle, there are certain regularities in nature and identical causes always lead to identical effects. But since nature is uniform, so the argument goes, we don’t need to observe millions of objects of the same class. It would suffice to observe a few objects of the same class, to note what they have in common and then safely generalize that to all objects of that class. This generalization would hold because nature is uniform, i.e. because identical initial conditions always produce identical effects. According to this line of reasoning, we don’t need to observe all swans in the world to prove that all of them are white. They are all white because the ones we have observed so far have all been white and because the principle of uniformity tells us that all swans are similar as they are all products of the same biological mechanism. By the same token, there is no need to test the law of gravity for every pair of objects in the universe, since according to the principle of uniformity all objects with mass must act similarly. In short, the principle allows to safely extrapolate from past experience to all cases of the same class and to ensure that there won’t be any surprises in the future:

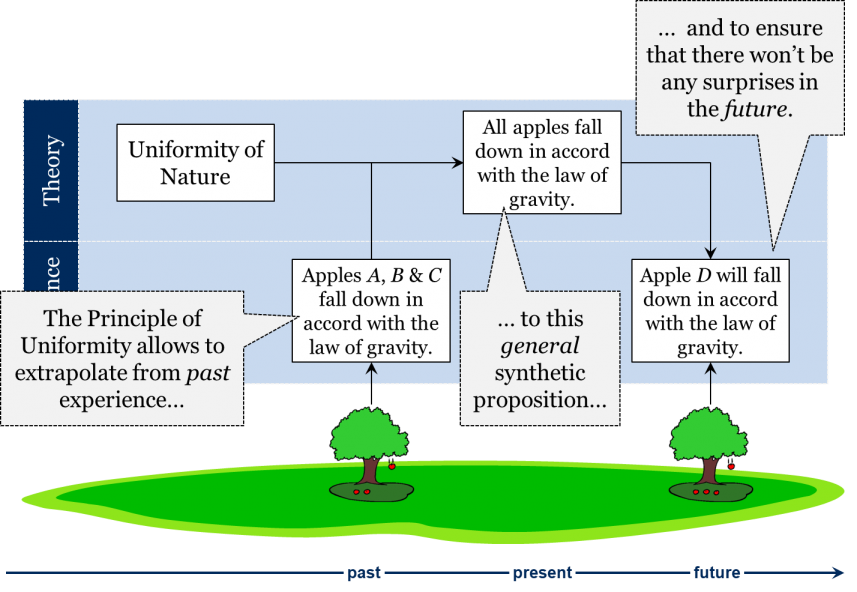
With this wonderful principle of the uniformity of nature, we are no longer required to make an infinite number of observations to prove a general synthetic proposition.

Now, does this solution hold water? It is true that if the principle of uniformity were established beyond any reasonable doubt, then it would solve our problem. But how do we know that nature is regular and uniform? How is the principle of uniformity itself justified? There are two options here.

Option 1: We can try to argue that the principle itself is an analytic proposition, i.e. that it is true by definition. But this is not a viable option: the principle of uniformity is not an analytic proposition, since its opposite is conceivable. For instance, we can easily conceive of a world where regularities allow for exceptions. We can equally conceive of a world with no regularities whatsoever. Clearly, the principle of uniformity itself is a synthetic proposition – it is a hypothesis about the workings of our world. This leaves the second option.

Option 2: We can try to argue that, as a general synthetic proposition, the principle of uniformity is justified through thousands of years of human experience. We see regularities everywhere around us and we see that these regularities don’t change through time: apples have been falling to the ground since time immemorial and they still fall down just fine. Thus, the principle of uniformity is based on our observations that in similar conditions objects of the same type have always behaved similarly. In other words, the principle is itself an inductive generalization of our past experience: it assumes that objects of the same type will always behave similarly because that’s how they have behaved so far. Thus, the principle of uniformity faces the same problem as any other general synthetic proposition – the problem of induction.

Therefore, we cannot solve the problem of induction by means of the principle of uniformity, because that would lead to a vicious circle: we would use the principle of uniformity to guarantee the absolute certainty of our inductive generalizations, but we would also use induction to justify the principle of uniformity itself, which we would then use to justify induction, which would then justify the principle of uniformity, and so on. We would end up in a vicious circle!

It is accepted nowadays that the problem of induction doesn’t have a perfect solution and, therefore, our inductive generalizations based on limited experience are fallible. Of course, this doesn’t mean we have to stop making inductive generalizations; all it suggests is that these generalizations are not absolutely certain. We cannot and should not avoid drawing general conclusions; we just have to appreciate that they are not proven beyond any reasonable doubt.

Problem 3: Theory-Ladenness

Let’s now proceed to our third problem – the problem of the theory-ladenness of observations. Consider the following image:

What do we see here? Those of us without astronomical training will probably see some stars obscured by what seems to be a cloud of poisonous gas. However, people trained in astronomy would most likely say that this is the Pillars of Creation, a photograph of interstellar gas and dust about 7000 light-years from Earth in the Eagle Nebula. In other words, our observation of the Pillars of Creation is laden with our astronomical theories. This phenomenon is known as the theory-ladenness of observations.

It is nowadays accepted that all observations are theory-laden, i.e. they depend on some accepted theories. Another way of saying the same thing is that there are no pure statements of fact, in the sense that all statements of fact presuppose one theory or another. Note that here “pure” means “unaffected by any theory”. The point is that no observational statement is pure: all observational statements are shaped by one theory or another.

Consider another image:

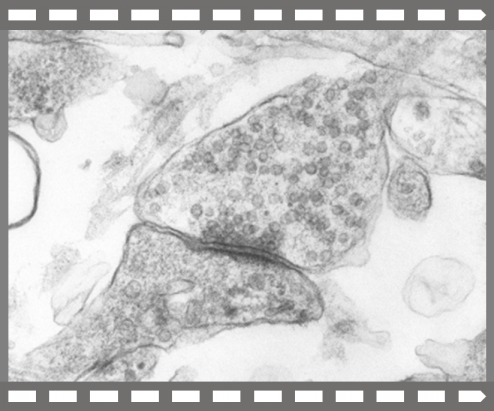
What is this? While a layman will probably see a fuzzy greyish picture, a person educated in neurophysiology will see a synapse. More specifically, an educated person will see a presynaptic terminal in the upper right portion of the image and a postsynaptic terminal in the lower left. They will recognize the presynaptic terminal by the small dark circles it contains. They will see these circles as packets of neurotransmitter molecules called synaptic vesicles. These vesicles can release neurotransmitter into the thin gap between the presynaptic terminal and the postsynaptic terminal, which is called the synaptic cleft. Neurotransmitter molecules can cross this gap and bind chemically to receptor molecules on the postsynaptic terminal. But this understanding is only possible if we accept some of the theories of neurophysiology. This is another example of our accepted theories shaping the results of our observations.

The general point here is that all propositions that describe our experience are inevitably theory-laden: there are no pure statements of fact.

To appreciate this point, let’s take another example. Suppose we look at the Moon through a telescope and observe that it has mountains. Why is this not a pure statement of fact? The proposition “there are mountains on the moon” is not a pure statement of fact because it assumes the reliability of the telescope. But the reason we rely on the telescope is because we know that it was constructed in accord with our accepted optical theory which suggests that a certain combination of magnifiers produces a trustworthy image.

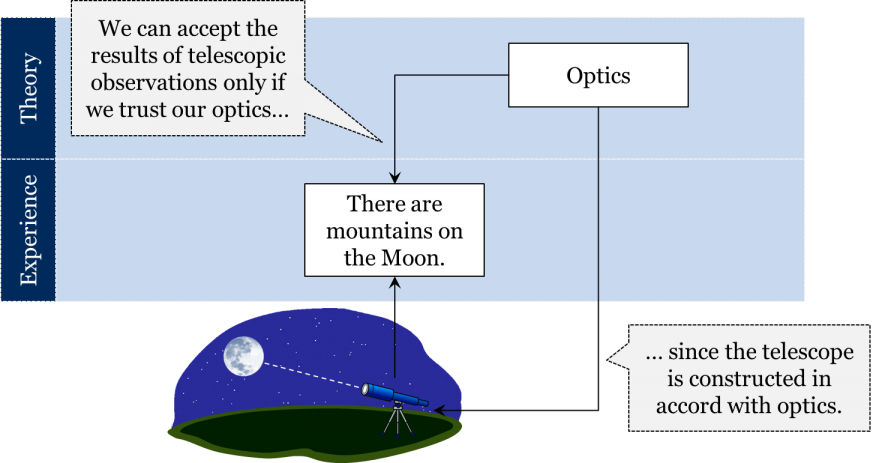
Generally speaking, any observational instrument presupposes one theory or another and, therefore, the observational results obtained by means of an instrument depend on the theories in accordance with which the instrument is constructed.

But what about those cases where we don’t seem to use any instruments? Suppose I look out the window with my naked eye and say, “it’s raining”. How is this proposition theory-laden? Surely, I am not using any instruments, so what theories are presupposed here? Even in this most simple case, my observation is based on some basic assumptions about my own physiology and about optics. In fact, we do not trust our observations at all times, but only when they satisfy certain basic criteria, such as proper illumination, the absence of visual obstacles such as fog, not having taken a hallucinogenic drug, nor subject to hallucinations due to malnourishment or sickness, etc. For instance, when a teaspoon appears bent or broken in a glass of water, we don’t trust this sensation, for we have some prior knowledge of how these things work. We essentially rely on some basic experiential knowledge of optics.

Once again, it doesn’t matter that these theories often remain unarticulated; what matters is that any observation – even a naked-eye observation – is based on some theoretical assumptions. At the very minimum, there are some physiological and optical assumptions that allow us to determine which sensations to trust and which not to trust. Thus, there are no pure statements of fact; all observations are theory-laden.

The problem of theory-ladenness becomes especially daunting once we appreciate that the theories through which we see the world change through time. Effectively, the same image can be interpreted differently depending on which set of theories we use to interpret it. Consider the example of a falling apple. Where Aristotelians would see a heavy object composed predominantly of the elements earth and water descending towards the centre of the universe, Newtonians would see a gravitational attraction between the Earth and the apple. In contrast, nowadays we would interpret this as a case of inertial of motion in the curved space-time continuum produced by the Earth’s mass. Similarly, where chemists of the mid-18th century would see dephlogisticated air, we would see oxygen. The same goes for any observation in any field of inquiry.